Stochastic Gradient Descent, Momentum, AdaGrad, and Adam
Date : 2022.10.11
*The contents of this book is heavily based on Stanford University’s CS231n course.
Optimization is the process of finding the optimal variable value. We will explore different methods of optimization to initialize hyperparameters and input variables.
The purpose of these “methods” is to increase both efficiency and accuracy of the CNN.
[Optimization]
There is no short-cut or ‘easy’ way of optimizing variables. Complex networks require higher time and space complexity. We already had a taste of one of the optimization methods. SGD uses differentiation of the variable loss function to find the optimal weight variable.
[SGD]
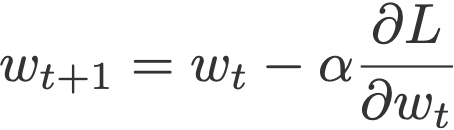
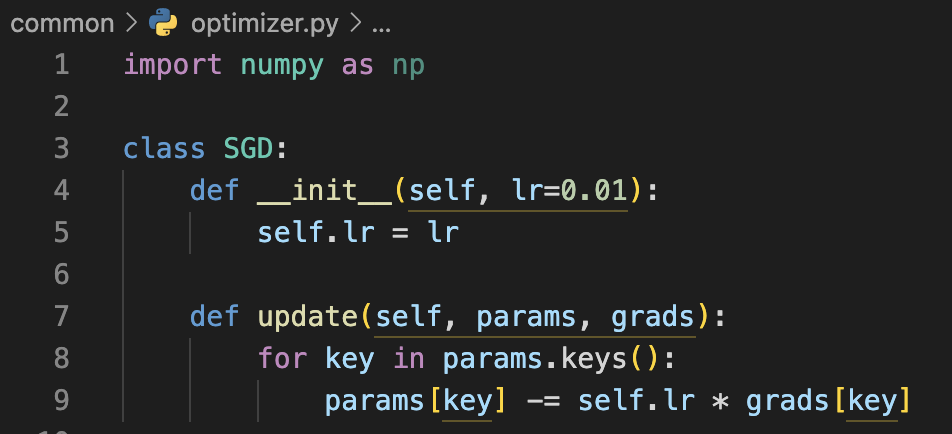
By separating different optimization methods into independent classes (objects), we can use each method like modules. SGD may not be the best method of optimization. For example SGD is relatively less efficient when it comes to anisotropy functions.

We shall explore some other options.
[Momentum]

𝑣 is the velocity and 𝑝 is the resistance.


Compared to SGD, the momentum method has a smoother curvature heading towards the minimum point. The velocity variable pulls the x variable faster. Similar to a ball falling towards the bottom, the x-axis follows along a relatively fixed path (straight line), thus the velocity factor adds speed (greater descent) compared to y.
[AdaGrad]
The learning rate is an essential part of optimizing the weight variable. Thus, we will use ‘Learning Rate Decay’ which is an efficient way of selecting and updating the learning rate. Learning rate decay method generally uses a high learning rate at the start and gradually decays the value as the network reaches higher accuracy. The AdaGrad method updates the learning rate for each weight variable by squaring the original learning rate.

It’s interesting how the new adaptive learning rate is part of the numerator. The h variable from line 1 measures the gradient descent for each variable. The greater the gradient, the more the learning rate decays.
“Gradient Descent Value Increases → Learning Rate Decay Factor Increases → Next Gradient Descent Value Decreases”


The optimization route shows a drastic decrease in the zig-zag pattern along the y-axis. After the first huge y-value gradient drop, the h variable significantly decreases the learning rate.
[Adam]
Adam is a combination of ‘momentum’ and ‘adagrad.’

…
I am skipping the comparison between different optimization methods because that is not a part of my key interest of building a CNN. The code for comparison is in the github link below. It is fairly easy to understand.
https://github.com/jk-junhokim/deep-learning-from-scratch/tree/master/ch06
'Tech Development > Deep Learning (CNN)' 카테고리의 다른 글
| Batch Initialization, Overfitting, Dropout, and Optimization (0) | 2022.12.16 |
|---|---|
| Weight Initialization, Xavier Weights, Dropout, and Setting Hyperparameters (0) | 2022.12.16 |
| Neural Network with Backward Propagation (0) | 2022.12.16 |
| Computational Graphs & Backward Propagation (0) | 2022.10.24 |
| SGD, Epochs, and Accuracy Testing (0) | 2022.10.22 |




댓글