Problem Solving with Algorithms and Data Structures 3.0 by Brad Miller, David Ranum
(A Summary of ADT’s, Trees, and Binary Search)
Date
2022.07.31
Trees
A tree data structure has a root, branches, and leaves. A tree data structure has its root at the top and its leaves on the bottom.
Vocabulary of Tree Structure
- Node : A node is a fundamental part of a tree. It can have a name, which we call the “key.” A node may also have additional information called “payload.”
- Edge : An edge connects two nodes to show that there is a relationship between them.
- Root : The root of the tree is the only node in the tree that has no incoming edges.
- Path : A path is an ordered list of nodes that are connected by edges.
- Children : The set of nodes that have incoming edges from the same node are said to be the children of that node.
- Parent : A node is the parent of all the nodes it connects to with outgoing edges.
- Sibling : Nodes in the tree that are children of the same parent are siblings.
- Height : The height of a tree is equal to the maximum level of any node in the tree.

Definition of Tree
A tree consists of a set of nodes and a set of edges that connect pairs of nodes. A tree has the following properties:
- One node of the tree is designated as the root node.
- Every node n, except the root node, is connected by an edge from exactly one other node p, where p is the parent of n.
- A unique path traverses from the root to each node.
- If each node in the tree has a maximum of two children, we say that the tree is a binary tree.
Implementation of Binary Tree
- BinaryTree() creates a new instance of a binary tree.
- get_left_child() returns the binary tree corresponding to the left child of the current node.
- get_right_child() returns the binary tree corresponding to the right child of the current node.
- set_root_val(val) stores the object in parameter val in the current node.
- get_root_val() returns the object stored in the current node.
- insert_left(val) creates a new binary tree and installs it as the left child of the current node.
- insert_right(val) creates a new binary tree and installs it as the right child of the current node.
List of Lists Representation
In a tree represented by a list of lists, we will begin with Python’s list data structure and write the functions defined above.

Nodes and References
In this case we will define a class that has attributes for the root value, as well as the left and right subtrees. Since this representation more closely follows the object-oriented programming paradigm, we will continue to use this representation.
Both the left and right children of the root are themselves distinct instances of the BinaryTree class. As we said in our original recursive definition for a tree, this allows us to treat any child of a binary tree as a binary tree itself.

Priority Queues with Binary Heaps
In a priority queue the logical order of items inside a queue is determined by their priority. The highest priority items are at the front of the queue and lowest priority items are at the back. The class way to implement a priority queue is using a data structure called a binary heap. A binary heap will allow us both enqueue and dequeue items in O(log n). The binary heap has two common variations: the min heap, in which the smallest key is always at the front, and the max heap, in which the largest key value is always at the front.
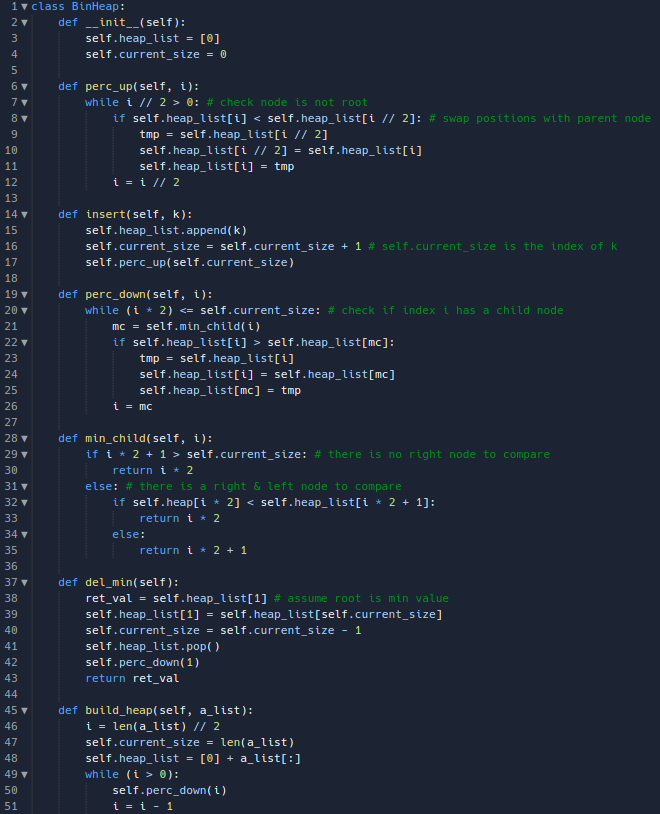
Binary Heap Operations
The basic operations we will implement for our binary heap are as follows:
- BinaryHeap() creates a new, empty, binary heap.
- insert(k) adds a new item to the heap.
- find_min() returns the item with the minimum key value, leaving the item in the heap.
- del_min() return the item with the minimum key value, removing the item from the heap.
- is_empty() returns true if the heap is empty, false otherwise.
- size() returns the number of items in the heap.
- build_heap(list) builds a new heap from a list of keys.
Binary Heap Implementation
We will take advantage of the logarithmic nature of the binary tree to represent our heap. A complete binary tree is a tree in which each level has all of its nodes. The exception to this is the bottom level of the tree, which we fill in from the left to right.
When the tree is complete, the left child of the parent (at position p) is the node that is found in position 2p in the list. Similarly, the right child of the parent is at position 2p+1 in the list. Given that a node is at position n in the list, the parent is at position n/2.
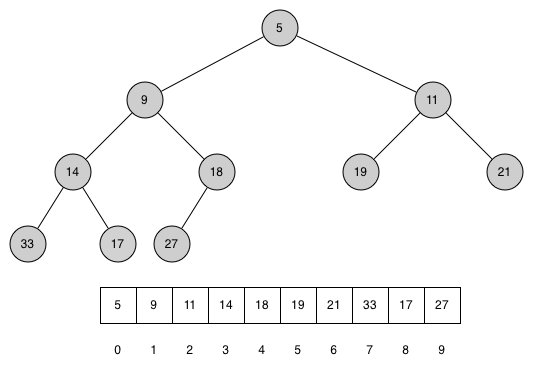
The Heap Order Property
In a heap, for every node x with parent p, the key in p is smaller than or equal to the key in x.
'Tech Development > Algorithms & Data Structures' 카테고리의 다른 글
| Problem Solving with Algorithms & Data Structures part 4/4 (0) | 2022.08.26 |
|---|---|
| Problem Solving with Algorithms & Data Structures part 3/4 (0) | 2022.08.24 |
| Problem Solving with Algorithms & Data Structures Part 1/4 (0) | 2022.08.10 |



댓글