Problem Solving with Algorithms and Data Structures 3.0 by Brad Miller, David Ranum
(A Summary ADT’s, Queue, Stack, and Deque)
Date
2022.07.27
Why Study Data Structures and Abstract Data Types?
An abstract data type, sometimes called an ADT, is a logical description of how we view the data and the operations that are allowed without regard to how they will be implemented. This means that we are concerned only with what the data is representing and not with how it will eventually be constructed. By providing this level of abstraction, we are creating an encapsulation around the data.
The user interacts with the interface, using the operations that have been specified by the abstract data type.
Stacks
Stacks are ordered LIFO.
The Stack Abstract Data Type
- Stack() creates a new stack that is empty. It needs no parameters and returns an empty stack.
- push(item) adds a new item to the top of the stack.
- pop() removes the top item from the stack. It needs no parameters and returns the item. The stack is modified.
- peek() returns the top item from the stack but does not remove it.
- is_empty() tests to see whether the stack is empty.
- size() return the number of items on the stack.
Python, as in any object-oriented programming language, the implementation of choice for an abstract data type such as a stack is the creation of a new class. The stack operations are implemented as methods.
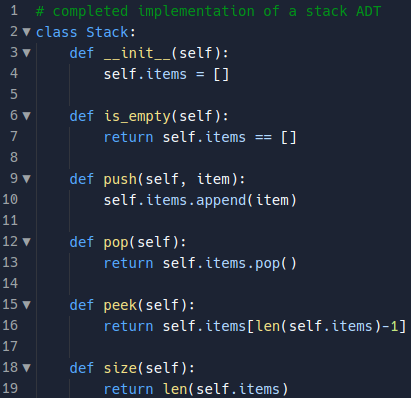
We must create a Stack object and then use it.
Queues
This ordering principle is called FIFO.
The Queue Abstract Data Type
- Queue() creates a new queue that is empty. It needs no parameters and returns an empty queue.
- enqueue(item) adds a new item to the rear of the queue. It needs the item and returns nothing.
- dequeue() removes the front item from the queue.
- is_empty() tests to see whether the queue is empty.
- size() returns the number of items in the queue.

Simulation: Printing Tasks
Recall that as students send printing tasks to the shared printer, the tasks are placed in a queue to be processed in the first-come first-served manner. The most important of these might be whether the printer is capable of handling a certain amount of work. We will need to construct representations for students, printing tasks, and the printer. Of interest for us is the average amount of time students will wait for their papers to be printed. This is equal to the average amount of time a task waits in the queue.
Simulation Recipe
1. Create a queue of print tasks. Each task will be given a timestamp upon its arrival. The queue is empty to start.
2. For each second (current_second):
- Does a new print task get created? If so, add it to the queue with the current_second as the timestamp.
- If the printer is not busy and if a task is waiting.
- Remove the next task from the print queue and assign it to the printer.
- Subtract the timestamp from the current_second to compute the waiting time for that task.
- Append the waiting time for that task to a list for later processing.
- Based on the number of pages in the print task, figure out how much time will be required.
- The printer now does one second of printing if necessary. It also subtracts one second from the time required for that task.
- If the task has been completed, in other words the time required has reached zero, the printer is no longer busy.
3. After the simulation is complete, compute the average waiting time from the list of waiting times generated.


The Simulation

The Results
Deque
A deque, also known as a double-ended queue, is an ordered collection of items similar to the queue. What makes a deque different is the unrestrictive nature of adding and removing items. New items can be added at either the front or the rear. Likewise, existing items can be removed from either end.
The Deque Abstract Data Type
- Deque() creates a new deque that is empty.
- add_front(item) adds a new item to the front of the deque.
- add_rear(item) adds a new item to the rear of the deque.
- remove_front() removes the front item from the deque.
- remove_rear() removes the rear item from the deque.
- is_empty() tests to see whether the deque is empty.
- size() returns the number of items in the deque.

'Tech Development > Algorithms & Data Structures' 카테고리의 다른 글
| Problem Solving with Algorithms & Data Structures part 4/4 (0) | 2022.08.26 |
|---|---|
| Problem Solving with Algorithms & Data Structures part 3/4 (0) | 2022.08.24 |
| Problem Solving with Algorithms & Data Structures part 2/4 (0) | 2022.08.24 |



댓글